自动微分

约 4037 个字 39 行代码 14 张图片预计阅读时间 14 分钟

Part 1: 微分方法简介

微分在机器学习中的作用

首先，我们回顾一下，任何一个机器学习算法都包含三个核心部分。微分，尤其是梯度计算，在其中扮演着至关重要的角色。

|364

假设类别 (The hypothesis class):
* 这是我们模型的结构，比如一个神经网络。它定义了输入 \(x\) 如何被参数 \(\theta\) 转换为输出 \(h_\theta(x)\)。
损失函数 (The loss function):
* 它用于衡量模型预测 \(h_\theta(x)\) 与真实标签 \(y\) 之间的差距。一个常见的例子是交叉熵损失函数：
* \(l(h_\theta(x), y) = -h_y(x) + \log \sum_{j=1}^{k} \exp(h_j(x))\)
优化方法 (An optimization method):
* 这是我们用来调整参数 \(\theta\) 以最小化损失函数的方法，最常用的方法是梯度下降，在实际中我们常常选取一个mini-batch，实行SGD（Stochastic Gradient Descent）
* \(\theta := \theta - \frac{\alpha}{B} \sum_{i=1}^{B} \nabla_\theta l(h_\theta(x^{(i)}), y^{(i)})\)
* 在这个更新规则中，最核心的部分就是计算损失函数关于参数 \(\theta\) 的梯度 \(\nabla_\theta l\)。

微分方法一：数值微分 (Numerical Differentiation)

数值微分是最直观的求导方法，它直接利用导数的定义来近似计算。

基本定义法：
根据导数的定义，我们可以用一个很小的 \(\epsilon\) 来近似计算偏导数：
\(\frac{\partial f(\theta)}{\partial \theta_i} = \lim_{\epsilon \to 0} \frac{f(\theta + \epsilon e_i) - f(\theta)}{\epsilon}\)
其中 \(e_i\) 是一个独热向量（one-hot vector），在第 \(i\) 个位置为1，其余为0。

中心差分法（更精确）：
为了获得更高的数值精度，我们可以使用中心差分公式，它的误差是 \(\epsilon^2\) 级别的，比基本定义法的 \(\epsilon\) 级别误差要小。
\(\frac{\partial f(\theta)}{\partial \theta_i} = \frac{f(\theta + \epsilon e_i) - f(\theta - \epsilon e_i)}{2\epsilon} + O(\epsilon^2)\)

Tip

为什么误差更小？—— Taylor Expansion
\(f(\theta+\delta)=f(\theta)+f'(\theta)\delta+\frac{1}{2}f''(\theta)\delta^2+O(\delta^3)\)
\(f(\theta-\delta)=f(\theta)-f'(\theta)\delta+\frac{1}{2}f''(\theta)\delta^2-O(\delta^3)\)
\(\Rightarrow f(\theta + \delta) - f(\theta - \delta) = 2f'(\theta)\delta + O(\delta^3), \quad \quad \frac{f(\theta + \delta) - f(\theta - \delta)}{2\delta} = f'(\theta) + \frac{O(\delta^3)}{2\delta}\)
因此有 \(f'(\theta) = \frac{f(\theta + \delta) - f(\theta - \delta)}{2\delta} + O(\delta^2)\)

数值微分的缺点

数值误差 (Numerical Error): 结果是一个近似值，\(\epsilon\) 的选择会严重影响精度。太大会导致近似不准，太小会引起舍入误差。
计算效率低 (Less Efficient): 为了计算每个参数 \(\theta_i\) 的偏导数，都需要至少调用函数 \(f\) 两次。如果模型有百万个参数，就需要进行两百万次函数评估，计算量巨大。

数值梯度检查 (Numerical Gradient Checking)

尽管数值微分不适合在模型训练中直接使用，但它是一个非常强大的验证工具。我们可以用它来检查我们实现的更复杂的微分算法（比如自动微分）是否正确。

如何进行梯度检查

我们可以通过下面的公式来验证梯度计算的正确性：
\(\delta^T \nabla_\theta f(\theta) = \frac{f(\theta + \epsilon\delta) - f(\theta - \epsilon\delta)}{2\epsilon} + O(\epsilon^2)\)

步骤：

从一个单位球（unit ball）中随机选择一个很小的向量 \(\delta\)。
分别计算等式的左边（用你实现的算法计算梯度 \(\nabla_\theta f(\theta)\)，然后与 \(\delta\) 做点积）和右边（用数值微分公式计算）。
比较两边的结果是否足够接近。如果对于多个随机的 \(\delta\) 两边都相等，那么我们实现的梯度算法就很可能是正确的。

微分方法二：符号微分 (Symbolic Differentiation)

符号微分是我们上学时学习的求导方法，即对数学表达式应用求导法则（如和、积、链式法则）来推导出梯度的精确表达式。

基本法则：
* 和法则: \(\frac{\partial(f(\theta)+g(\theta))}{\partial\theta} = \frac{\partial f(\theta)}{\partial\theta} + \frac{\partial g(\theta)}{\partial\theta}\)
* 积法则: \(\frac{\partial(f(\theta)g(\theta))}{\partial\theta} = g(\theta)\frac{\partial f(\theta)}{\partial\theta} + f(\theta)\frac{\partial g(\theta)}{\partial\theta}\)
* 链式法则: \(\frac{\partial f(g(\theta))}{\partial\theta} = \frac{\partial f(g(\theta))}{\partial g(\theta)} \frac{\partial g(\theta)}{\partial\theta}\)

符号微分的缺点

简单地、机械地应用这些规则可能会导致表达式膨胀 (expression swell) 和 计算浪费 (wasted computations)。

符号微分的计算浪费

假设我们有函数 \(f(\theta) = \prod_{i=1}^{n} \theta_i = \theta_1 \times \theta_2 \times \dots \times \theta_n\)。

我们想要求解它对每个 \(\theta_k\) 的偏导数：
\(\frac{\partial f(\theta)}{\partial \theta_k} = \prod_{j \neq k} \theta_j\)

如果我们为每个 \(k\) (从1到n) 都独立地计算这个乘积，那么每次计算都需要 \(n-2\) 次乘法。计算所有 \(n\) 个偏导数总共需要的乘法次数为 \(n \times (n-2)\)。

这是一个巨大的浪费！因为很多子表达式（例如 \(\theta_1 \times \theta_2\)）在计算不同偏导数时被重复计算了。

微分方法三：自动微分 (Automatic Differentiation, AD)

自动微分结合了符号微分和数值微分的优点。它不是直接操作数学表达式，而是作用于计算过程本身。

计算图 (Computational Graph)

任何复杂的计算过程都可以被分解为一系列基本运算，并用一个有向无环图（Direct Acyclic Graph, DAG）来表示，这就是计算图。

计算图的构成

节点 (Node): 代表计算中的一个（中间）值。例如输入变量 \(x_1, x_2\) 或中间结果 \(v_3, v_4\)。
边 (Edge): 代表节点之间的输入/输出关系，通常对应一个基本运算（如 ln, +, *, sin）。

计算图的前向评估

让我们以前向评估（Forward Evaluation）的方式，一步步计算函数 \(y = f(x_1, x_2) = \ln(x_1) + x_1 x_2 - \sin(x_2)\) 在 \(x_1=2, x_2=5\) 时的值。

\(v_1 = x_1 = 2\)
\(v_2 = x_2 = 5\)
\(v_3 = \ln(v_1) = \ln(2) = 0.693\)
\(v_4 = v_1 \times v_2 = 2 \times 5 = 10\)
\(v_5 = \sin(v_2) = \sin(5) = -0.959\)
\(v_6 = v_3 + v_4 = 0.693 + 10 = 10.693\)
\(v_7 = v_6 - v_5 = 10.693 - (-0.959) = 11.652\)
\(y = v_7 = 11.652\)

这个过程就是我们平时程序执行的过程，也叫前向传播 (Forward Propagation)。

前向模式自动微分 (Forward Mode AD)

前向模式 AD 的核心思想是：在进行前向评估的同时，计算每个中间变量对于某一个输入变量的导数。

关键定义

我们定义 \(\dot{v_i} = \frac{\partial v_i}{\partial x_1}\)，这个 "点" 符号代表 \(v_i\) 对我们关心的某一个输入（这里是 \(x_1\)）的导数。

前向模式 AD 示例

我们来计算 \(\frac{\partial y}{\partial x_1}\)。我们需要按照计算图的拓扑顺序，依次计算每个节点的 \(\dot{v_i}\)。

前向 AD 轨迹 (Forward AD trace):

\(\dot{v_1} = \frac{\partial v_1}{\partial x_1} = \frac{\partial x_1}{\partial x_1} = 1\)
\(\dot{v_2} = \frac{\partial v_2}{\partial x_1} = \frac{\partial x_2}{\partial x_1} = 0\) (因为 \(x_2\) 与 \(x_1\) 无关)
\(v_3 = \ln(v_1) \implies \dot{v_3} = \frac{\partial v_3}{\partial v_1}\frac{\partial v_1}{\partial x_1} = \frac{1}{v_1} \dot{v_1} = \frac{1}{2} \times 1 = 0.5\)
\(v_4 = v_1 v_2 \implies \dot{v_4} = \frac{\partial v_4}{\partial v_1}\dot{v_1} + \frac{\partial v_4}{\partial v_2}\dot{v_2} = v_2 \dot{v_1} + v_1 \dot{v_2} = 5 \times 1 + 2 \times 0 = 5\)
\(v_5 = \sin(v_2) \implies \dot{v_5} = \cos(v_2) \dot{v_2} = \cos(5) \times 0 = 0\)
\(v_6 = v_3 + v_4 \implies \dot{v_6} = \dot{v_3} + \dot{v_4} = 0.5 + 5 = 5.5\)
\(v_7 = v_6 - v_5 \implies \dot{v_7} = \dot{v_6} - \dot{v_5} = 5.5 - 0 = 5.5\)

最终结果： 我们得到了 \(\frac{\partial y}{\partial x_1} = \dot{v_7} = 5.5\)

前向模式 AD 的局限性

对于一个函数 \(f: \mathbb{R}^n \to \mathbb{R}^k\)（\(n\) 个输入, \(k\) 个输出），前向模式 AD 每一次前向传播只能计算出所有输出相对于一个输入的梯度。

要计算完整的雅可比矩阵（所有输出对所有输入的梯度），我们需要进行 \(n\) 次前向传播。

在深度学习中，我们通常关心的是 \(k=1\)（一个标量损失函数）和非常大的 \(n\)（数百万的模型参数）。在这种情况下，前向模式需要进行 \(n\) 次传播，效率极低。

Part 2: 反向模式自动微分 (Reverse Mode AD)

为了解决前向模式在机器学习场景下的低效问题，我们引入了反向模式自动微分，它更为人熟知的名字是反向传播 (Backpropagation)。

关键定义

我们定义伴随 (adjoint) 变量 \(\bar{v_i} = \frac{\partial y}{\partial v_i}\)，它代表最终输出 \(y\) 对任意中间变量 \(v_i\) 的导数。

反向模式 AD 的核心思想是：在完成前向评估后，从最终输出开始，反向遍历计算图，计算出最终输出 \(y\) 对所有中间变量和输入变量的梯度。

反向模式 AD 示例

我们的目标是计算 \(\frac{\partial y}{\partial x_1}\) 和 \(\frac{\partial y}{\partial x_2}\)。

第一步：前向评估
这和之前的例子一样，计算出所有 \(v_i\) 的值。

第二步：反向 AD 轨迹 (Reverse AD evaluation trace)
我们从最后一个节点开始，以计算图的逆拓扑顺序进行计算。

\(\bar{v_7} = \frac{\partial y}{\partial v_7} = 1\) (输出对自身的导数永远是1，这是起点)
\(v_7 = v_6 - v_5 \implies \bar{v_6} = \frac{\partial y}{\partial v_6} = \frac{\partial y}{\partial v_7}\frac{\partial v_7}{\partial v_6} = \bar{v_7} \times 1 = 1\)
\(v_7 = v_6 - v_5 \implies \bar{v_5} = \frac{\partial y}{\partial v_5} = \frac{\partial y}{\partial v_7}\frac{\partial v_7}{\partial v_5} = \bar{v_7} \times (-1) = -1\)
\(v_6 = v_3 + v_4 \implies \bar{v_4} = \frac{\partial y}{\partial v_4} = \frac{\partial y}{\partial v_6}\frac{\partial v_6}{\partial v_4} = \bar{v_6} \times 1 = 1\)
\(v_6 = v_3 + v_4 \implies \bar{v_3} = \frac{\partial y}{\partial v_3} = \frac{\partial y}{\partial v_6}\frac{\partial v_6}{\partial v_3} = \bar{v_6} \times 1 = 1\)

处理多路径情况：
注意，节点 \(v_1\) 和 \(v_2\) 分别影响了 \(v_3\) 和 \(v_4\) 两个后续节点，所以它们的梯度是所有路径梯度的总和。

\(\bar{v_2} = \frac{\partial y}{\partial v_2} = \frac{\partial y}{\partial v_4}\frac{\partial v_4}{\partial v_2} + \frac{\partial y}{\partial v_5}\frac{\partial v_5}{\partial v_2} = \bar{v_4}\frac{\partial v_4}{\partial v_2} + \bar{v_5}\frac{\partial v_5}{\partial v_2}\)
\(\bar{v_2} = \bar{v_4} \times v_1 + \bar{v_5} \times \cos(v_2) = 1 \times 2 + (-1) \times \cos(5) = 2 - 0.284 = 1.716\)
\(\bar{v_1} = \frac{\partial y}{\partial v_1} = \frac{\partial y}{\partial v_3}\frac{\partial v_3}{\partial v_1} + \frac{\partial y}{\partial v_4}\frac{\partial v_4}{\partial v_1} = \bar{v_3}\frac{\partial v_3}{\partial v_1} + \bar{v_4}\frac{\partial v_4}{\partial v_1}\)
\(\bar{v_1} = \bar{v_3} \times \frac{1}{v_1} + \bar{v_4} \times v_2 = 1 \times \frac{1}{2} + 1 \times 5 = 5.5\)

最终结果： 经过一次反向传播，我们同时得到了 \(y\) 对所有输入的梯度！
\(\frac{\partial y}{\partial x_1} = \bar{v_1} = 5.5\)
\(\frac{\partial y}{\partial x_2} = \bar{v_2} = 1.716\)

多路径情况的推导

当一个节点 \(v_i\) 作为多个后续节点（例如 \(v_j\)）的输入时，根据多元链式法则，\(y\) 对 \(v_i\) 的总梯度等于 \(y\) 通过所有路径对 \(v_i\) 梯度的总和。

在上面的情况下，\(y=f(v_2,v_3)=f(v_1)\)

\(\therefore \bar{v}_1 = \frac{\partial y}{\partial v_1} = \frac{\partial f(v_2, v_3)}{\partial v_2} \frac{\partial v_2}{\partial v_1} + \frac{\partial f(v_2, v_3)}{\partial v_3} \frac{\partial v_3}{\partial v_1} = \bar{v}_2 \frac{\partial v_2}{\partial v_1} + \bar{v}_3 \frac{\partial v_2}{\partial v_1}\)

令 \(\bar{v}_{i \rightarrow j} = \bar{v}_j \frac{\partial v_j}{\partial v_i}\) ,则有 \(\bar{v}_i = \sum_{j \in \text{next}(i)} \bar{v_j} \frac{\partial v_j}{\partial v_i}\)

反向 AD 算法实现

我们可以用一个简单的伪代码来描述反向模式 AD 的算法流程。

def gradient(out_node):
    # node_to_grad 是一个字典，存储每个节点收到的部分伴随列表
    node_to_grad = {out_node: [1]} 

    # 按照计算图的逆拓扑顺序遍历所有节点
    for i in reverse_topo_order(out_node):

        # 1. 累加所有传入的部分伴随，得到该节点的总伴随（梯度）
        # 如果节点 i 不在 node_to_grad 中，说明没有路径指向它，梯度为0
        grad_i = sum(node_to_grad.get(i, [0])) 

        # 2. 遍历节点 i 的所有输入节点 k
        for k in inputs(i):

            # 3. 计算从 i 传播到 k 的部分伴随
            # grad_k_i = grad_i * (∂i / ∂k)
            partial_adjoint_k = grad_i * local_gradient(i, k)

            # 4. 将这个部分伴随“发送”给输入节点 k
            if k not in node_to_grad:
                node_to_grad[k] = []
            node_to_grad[k].append(partial_adjoint_k)

    # 返回所有输入节点的梯度
    return gradients_of_input_nodes

通过扩展计算图理解反向 AD

现代深度学习框架（如 PyTorch, TensorFlow）通常通过构建一个新的、反向的计算图来执行反向传播。我们可以通过一个例子来可视化这个过程。

|500

表达式：\((\exp(v_1)+1)\cdot \exp(v_1)\)

tab: 1
![](Pasted%20image%2020251209212050.png)

tab: 2
![](Pasted%20image%2020251209212103.png)

tab: 3
![](Pasted%20image%2020251209212112.png)

tab: 4
![](Pasted%20image%2020251209212122.png)

tab: 5
![](Pasted%20image%2020251209212131.png)

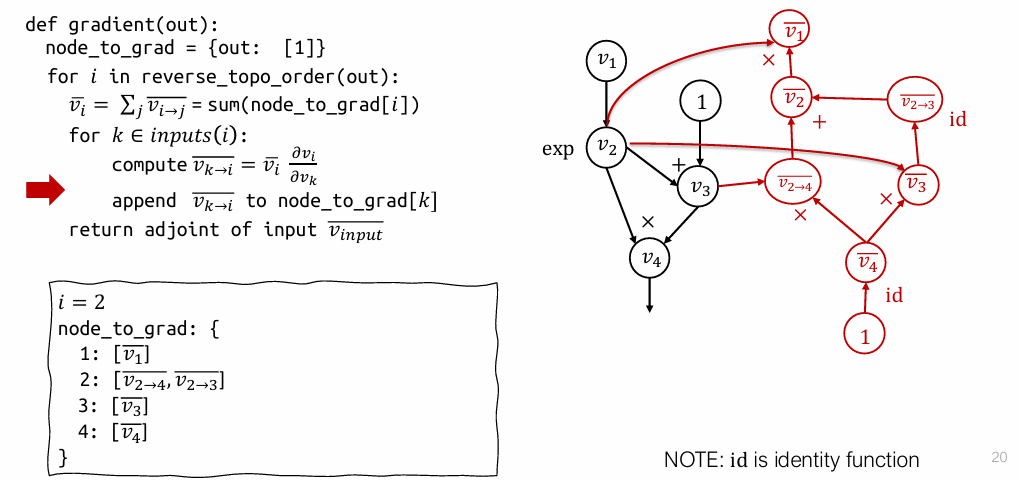
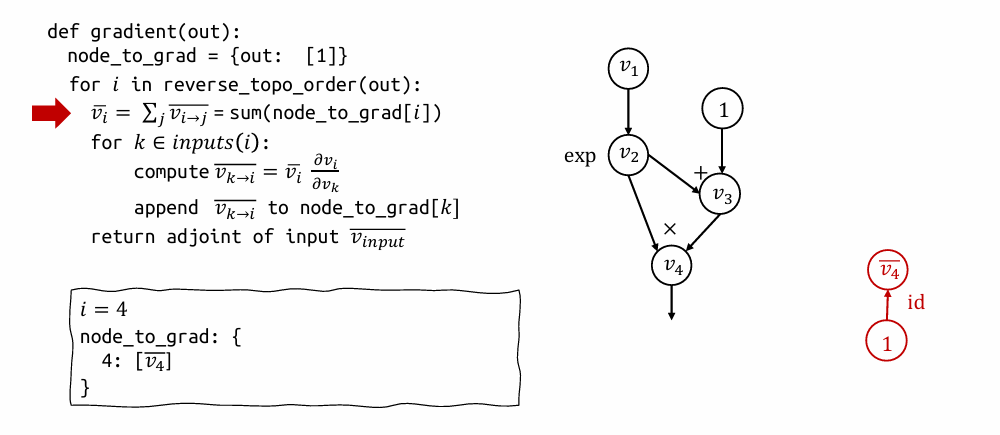
开始 (i=4): 从输出节点 \(v_4\) 开始，它的梯度是 1。node_to_grad 初始化为 {4: [1]}。
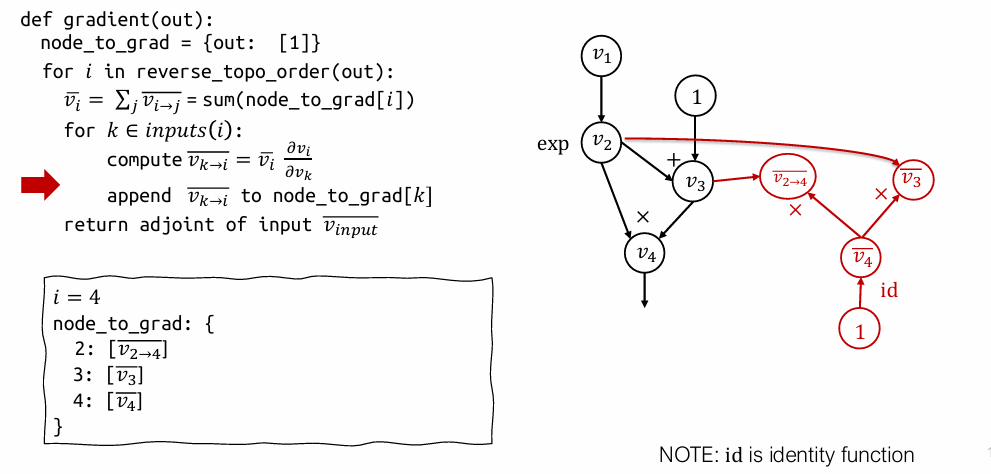
处理 \(v_4\): 将 \(v_4\) 的梯度 1 分别乘以局部导数 \(\frac{\partial v_4}{\partial v_2}\) 和 \(\frac{\partial v_4}{\partial v_3}\)，得到部分伴随 \(\bar{v}_{2 \to 4}\) 和 \(\bar{v}_{3 \to 4}\)，并将它们分别添加到 \(v_2\) 和 \(v_3\) 的梯度列表中。node_to_grad 变为 \(\{2: [ \bar{v}_{2 \to 4}], 3: [\bar{v}_{3 \to 4}], 4: [1]\}\)。
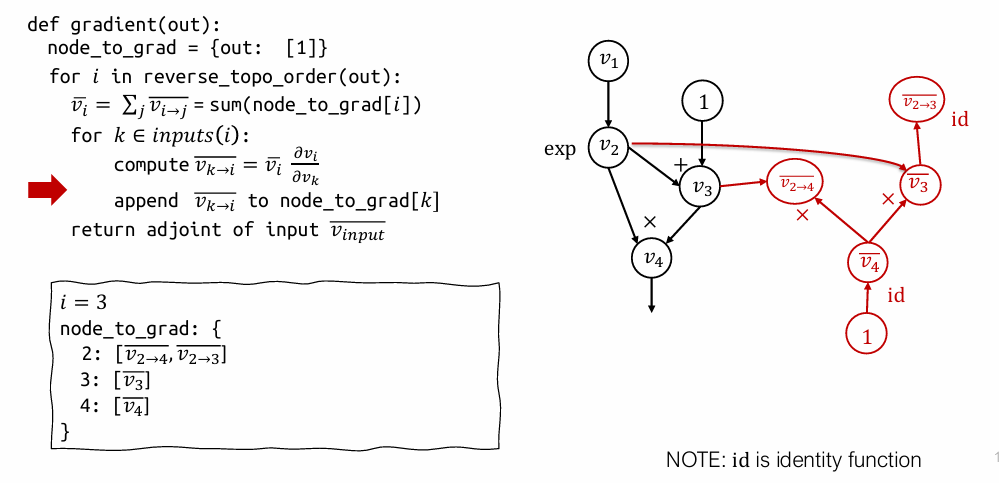
处理 \(v_3\) (i=3): 累加 node_to_grad[3] 得到 \(\bar{v_3}\)。然后计算 \(\bar{v_3}\) 对 \(v_3\) 的输入 \(v_2\) 的部分伴随 \(\bar{v}_{2 \to 3}\)，并将其添加到 node_to_grad[2] 中。此时 node_to_grad[2] 变为 [\bar{v}{2 \to 4}, \bar{v}]`。
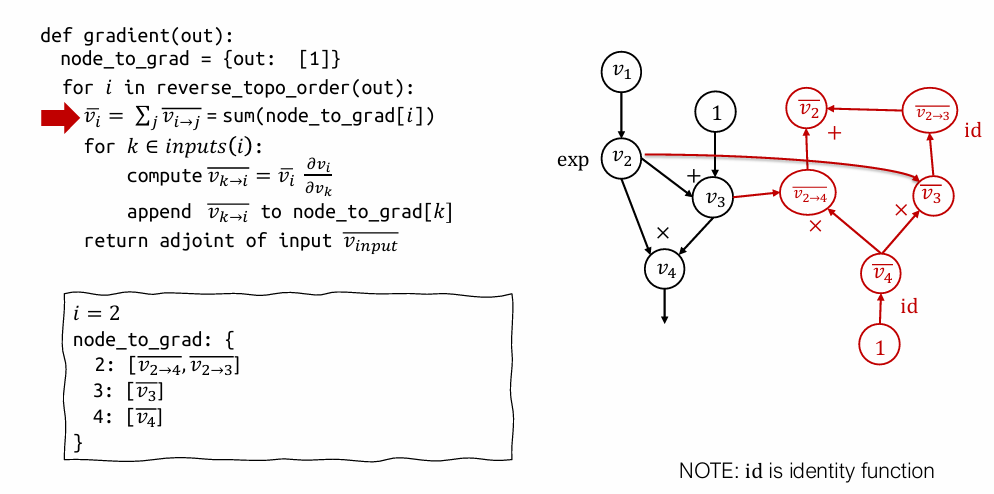
处理 \(v_2\) (i=2): 累加 node_to_grad[2] 中的两个部分伴随得到 \(\bar{v_2}\)。然后计算 \(\bar{v_2}\) 对 \(v_2\) 的输入 \(v_1\) 的部分伴随 \(\bar{v}_{1 \to 2}\)，并将其添加到 node_to_grad[1] 中。
结束。

这个过程实际上动态地构建了一个新的图（红色部分），这个新图的计算结果就是我们需要的梯度。

用处：通过计算图的运算，\(v_1 \rightarrow \bar{v_1}\),可以直接新建一个节点 \(\bar{v_1^2}\) ，跑一遍计算图，复用结果，而不是重算一遍。

可以通过优化计算图的方法来对计算进行优化。

反向模式 AD vs. 传统反向传播

两种实现方式

|575

传统反向传播 (Backprop):
* 在原始的前向计算图上运行反向操作。
* 这是第一代深度学习框架（如 Caffe, cuda-convnet）中使用的方式。
通过扩展图的反向模式 AD (Reverse mode AD by extending graph):
* 为伴随（梯度）构建独立的、分离的计算图节点。
* 这是现代深度学习框架（如 PyTorch, TensorFlow, Jax）中使用的方式，它更加灵活，例如可以轻松实现高阶导数。

在张量 (Tensors) 上的反向模式 AD

以上讨论都是基于标量，但深度学习中我们处理的都是张量（如向量、矩阵）。幸运的是，这些概念可以优雅地推广到张量运算。

前向传播:
* 标量形式: \(Z_{ij} = \sum_k X_{ik} W_{kj}\)
* 矩阵形式: \(Z = XW\)
* （后面可能跟着一个标量输出 \(v = f(Z)\)）

伴随定义:
* 张量 \(Z\) 的伴随 \(\bar{Z}\) 是一个与 \(Z\) 形状相同的张量，其中每个元素是 \(\bar{Z}_{ij} = \frac{\partial y}{\partial Z_{ij}}\)。

反向传播:
* 标量形式: \(\bar{X}_{ik} = \sum_j \frac{\partial Z_{ij}}{\partial X_{ik}} \bar{Z}_{ij} = \sum_j W_{kj} \bar{Z}_{ij}\)
* 矩阵形式: \(\bar{X} = \bar{Z} W^T\)
* 同样可以推导出: \(\bar{W} = X^T \bar{Z}\)

张量反向传播

对于矩阵乘法 \(Z=XW\)，其反向传播的梯度公式非常简洁，这使得在实践中实现起来非常高效。

进阶话题

梯度的梯度 (Gradient of Gradient)

现代 AD 系统的一个强大之处在于，反向传播的结果（即计算梯度的过程）本身也是一个计算图。这意味着我们可以对这个梯度图再次运行反向模式 AD，从而计算二阶导数（例如 Hessian 矩阵）。这对于一些高级优化算法和模型分析非常有用。

数据结构上的反向模式 AD

自动微分不仅可以应用于数值计算，还可以推广到包含数据结构（如字典、元组）的操作。

核心思想

关键在于为前向计算中的数据结构定义一个对应的伴随数据结构 (adjoint data structure)，并定义好伴随的传播规则。

例子：

前向: b = d["cat"] 从字典 d 中查找键 "cat" 对应的值。
伴随: 伴随值 \(\bar{b}\) 需要被“传播”回伴随字典 \(\bar{d}\) 中。传播规则是：将 \(\bar{b}\) 累加到 \(\bar{d}\) 中键为 "cat" 的位置上。

这使得自动微分框架能够支持更复杂的、非纯数学的程序结构。